
How do peopleĪctually do this in practice? That's a bit more complicated (Type I and Type II errors. State a significance level, you can pick one. Will state a specific significance level and you should use that. The values people usually use are 1%, 5%, orġ0% and it's called the "significance level" or alpha. The obvious next question is : "How small is small?" Different people might Reject the null hypothesis in favor of the alternative hypothesis and close So this is pretty strong evidence against the null hypothesis. Stronger is the evidence against the null hypothesis." p=0.0359 is pretty small. We are told "The smaller the p-value is, the Now we decide what the p-value means to us.

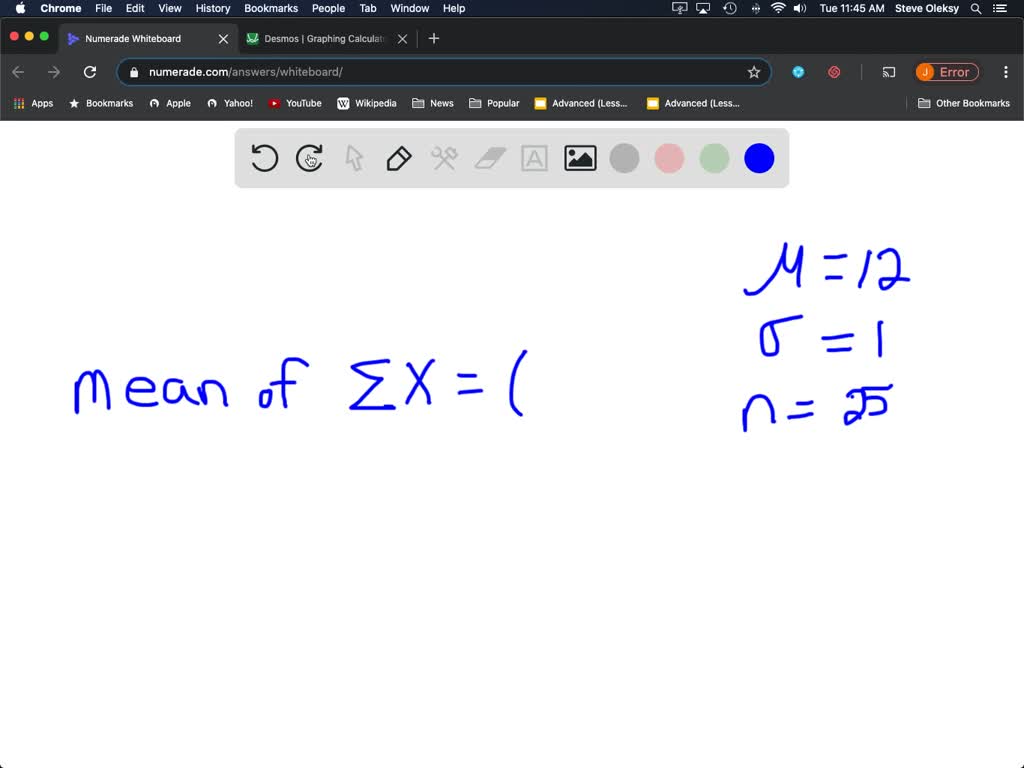
From the normal table, the area to the left of z=-1.80 is 0.0359. You could draw another picture with the z-score here if you need to. Now, to find that p-value, we just find the area. So shade in the area to the left of 299.1 on your picture. That means in the direction of the alternative hypothesis. When it says "as extreme or more extreme" The definition of p-value in your textbook. Now, we will shade in the area that corresponds to the p-value. Label it and draw a line to cut off the area below that value of x-bar. Xbar=299.1 is below the mean and not quite two standard deviations below it. Next, we must put the value of our test statistic on the graph of the sampling distribution of xbar. In summary, the sampling distribution of the test statistic is N(300,0.5). And, in the problem we were given that the population standard deviation, sigma, is equal to 3. Now, since we want to look at the sampling distribution of xbar when the null hypothesis is true, we see that specifies that mu=300. If the sample size is small, and if the population distribution is normally distributed then the distribution of xbar is normal with mean=mu and stdev=sigma/sqrt(n). Recalling the information from the Central Limit Theorem, we know that if the sample size is large enough, then no matter what the shape of the population distribution, the distribution of xbar is approximately normal, with mean=mu and stdev=sigma/sqrt(n).

Next we must determine the sampling distribution of the test statistic if the null hypothesis is true.
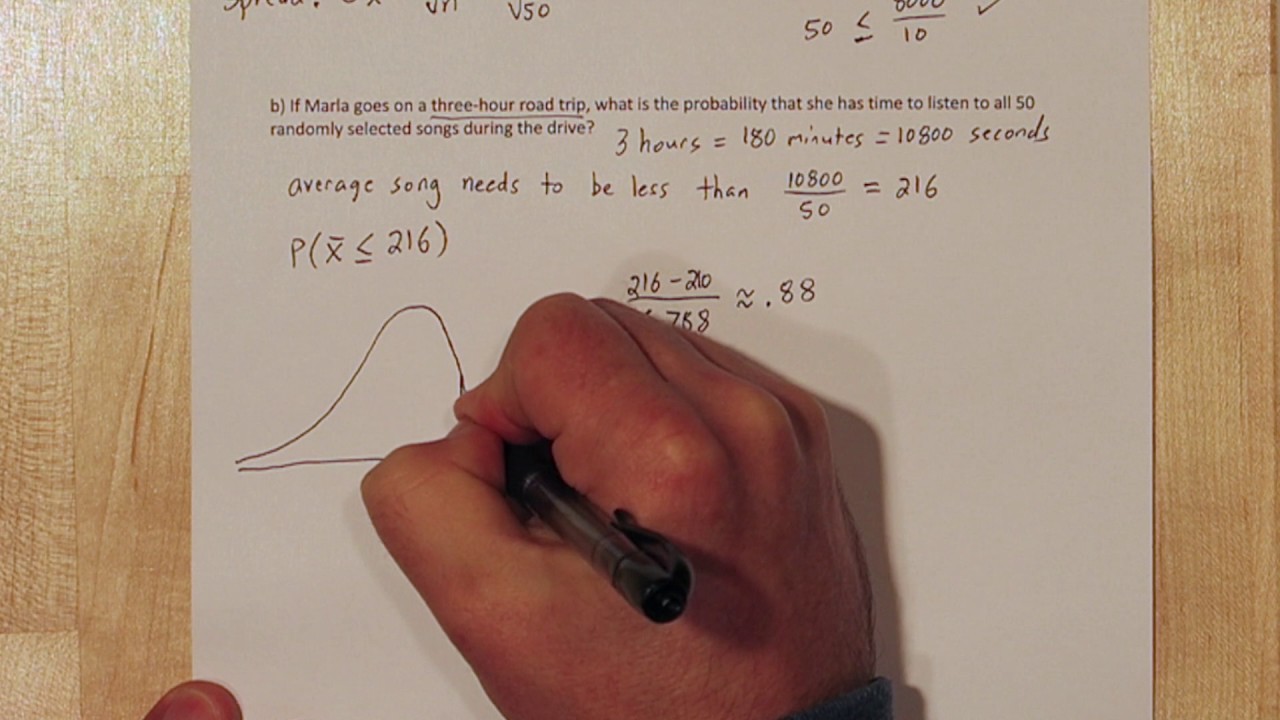
In this chapter and the next, we're testing hypotheses about the population mean, so it makes sense to use the sample mean, xbar. Next, we must determine what test statistic to use. We will use mu=300 for the null hypothesis. The null hypothesis can't overlap the alternative hypothesis and must have an "equal" in it. So the alternative hypothesis should be mu<300. This test is being done by an inspector who will "close down" the plant or at least close down the machine if he decides that the evidence significantly supports the claim that the population mean is less than 300 ml.įirst, what hypotheses will we use? As described in the section on writing hypotheses, the claim that will cause us to "change something" should be in the alternative hypothesis. and the population standard deviation is 3 ml. This is a continuation of the last example on this page and is based on the problem about the volume of cola in cola bottles.įor this example, I did a SRS of 36 bottles and found that xbar=299.1 ml.
#Sampling distribution of xbar how to#
(After you read this page, then see how to extend these ideas to a two-sided alternative hypothesis.)
#Sampling distribution of xbar full#
Full example of hypothesis testing: One-sided alternative hypothesis.


 0 kommentar(er)
0 kommentar(er)
